[Algorithm] BFS(Breadth First Search), DFS(Depth First Search)
블러드 필(Blood Fill)
다차원 배열에서 어떤 칸과 연결된 영역을 찾는 알고리즘
BFS(queue), DFS(stack)로 풀수 있음.
BFS(Breadth First Search)
- 다차원 배열에서 각 칸을 방문할 때 너비를 우선으로 방문하는 알고리즘.
- 모든 칸이 큐에 1번 씩만 들어감이 보장되므로 시간 복잡도는 칸이 N개 일때 O(N).
- 그래프 전체를 탐색하되, 인접한 노드들을 차례대로 방문.
- 그래프를 시작점을 루트로 하는 트리라고 생각한다면 height가 작은 노드부터 차례대로 방문하는 전체 탐색 방식이라고 할수 있음.
- 현재 보는 칸으로부터 추가되는 인접한 칸은 반드시 현재 보는 칸보다 시작점으로부터 1만큼 더 떨어져 있음. 이 성질을 이용해 시작점과의 거리를 저장할 dist배열을 하나 둠으로서 시작점에서 다른 모든 점으로 가는데 필요한 거리를 계산할 수 있음.
- 주의: queue에 push 할때 visited = true로 바꿔줘야함. queue에서 pop 할때 하면 안됨.

▶ 과정
1. 시작하는 칸을 큐에 push하고 방문했다는 표시를 남긴다.
2. 큐에서 원소를 pop해서 그 칸에 인접한 4개의 칸에 대해 3번의 행동을 한다.
3. 해당 칸을 이전에 방문했다면 아무 것도 하지 않고, 처음으로 방문했다면 방문했다는 표시를 남기고 해당 칸을 큐에 push한다.
4. 큐의 모든 원소가 빌 때 까지 2를 반복한다.
▶ 구현
while(queue가 비어있지 않다면)
{
1. queue의 가장 앞에 있는 노드를 pop
2. 현재 노드에 인접한 모든 노드들 중 아직 방문하지 않은 노드들을 queue에 push
}
DFS(Depth First Search)
- 다차원 배열에서 각 칸을 방문할 때 깊이를 우선으로 방문하는 알고리즘.
- 모든 칸이 큐에 1번 씩만 들어감이 보장되므로 시간 복잡도는 칸이 N개 일때 O(N).
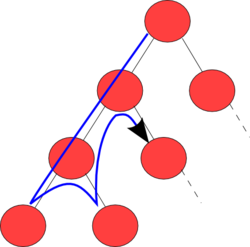
- 루트 노드에서 시작해서 다음 branch로 넘어가기 전에 해당 branch를 완벽하게 탐색하는 방법.
- 시작점으로 거리를 잴때는 DFS를 사용하면 안됨.
- 순환 호출을 이용해 풀 수 있음.
▶ 과정
1. 시작하는 칸을 스택에 push하고 방문했다는 표시를 남긴다.
2. 스택에서 원소를 pop해서 그 칸에 인접한 4개의 칸에 대해 3번의 행동을 한다.
3. 해당 칸을 이전에 방문했다면 아무 것도 하지 않고, 처음으로 방문했다면 방문했다는 표시를 남기고 해당 칸을 스택에 push한다.
4. 스택의 모든 원소가 빌 때 까지 2를 반복한다.
▶ 구현
순환 호출을 이용
function dfs(Node root)
{
1. root 노드 방문 후 방문했다고 표시
root.visited = true;
//root 노드와 인접한 노드를 모두 방문
for each (root 노드에 인접한 모든 노드 n에 대해)
{
2. 방문하지 않은 노드 n을 찾아서 해당 노드를 root 노드로 바꿔서 다시 dfs 함수를 시작(재귀)
if(n.visited == false) dfs(n);
}
}
참고
https://blog.encrypted.gg/729?category=773649
'CS > Algorithm 이론' 카테고리의 다른 글
| [Algorithm] priority queue (0) | 2020.05.03 |
|---|---|
| [Algorithm] 그래프(Graph) (0) | 2020.03.11 |
| [Algorithm] 전위/중위/후위 표기법(prefix/infix/postfix) (2) | 2020.01.31 |
| [Algorithm] 덱 (Deque) (0) | 2019.11.03 |
| [Algorithm] 큐 (Queue) (0) | 2019.10.30 |
![[Algorithm] BFS(Breadth First Search), DFS(Depth First Search)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbsJXxL%2FbtqBHyOyBfQ%2F16qGqhkQd6knNvI1rPncC0%2Fimg.png)